Cykloprůměr
Už se vám stalo, že jste šlapali na kole do nekonečného mírného kopce a zoufale sledovali tachometr, na kterém neúprosně svítilo číslo mnohem nižší, než průměr, který jste si pro vyjížďku stanovili? Určitě se pak vynořila otázka “Jak rychle budu muset jet zbytek trasy, abych průměr dohnal(a)?
Nedávno s tím v práci přišel šéf a jednoduchých intuitivních řešení se během chvilky objevilo hned několik. Mě se zdálo , že řešení bude jednoduchý lineární a vyřeší se to jen sčítáním a odčítáním. No a pak jsem si to napsal na papír.
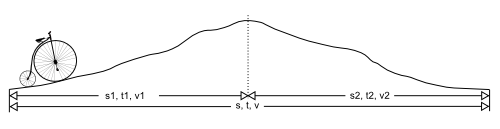
Zadání je na obrázku: známe délku celého úseku (s), délku ujetého úseku (s1), délku úseku, který zbývá (s2), průměrnou rychlost na celou trasu (v) a rychlost, kterou jsme projeli první úsek (v1). Co nás zajímá je v2 - tedy rychlost, jakou je třeba projet druhý úsek, aby celková průměrná rychlost byla v. Tady jsou rovnice, odvození a výsledný vztah:
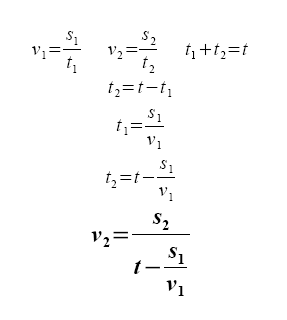
Pro demonstraci je tady konkrétní příklad, se kterým přišel šéf: celková délka trasy 20km (s), první úsek má 10 km (s1) a požadovaná průměrná rychlost na celou trasu je 20 km/h (v). Odpovídající hodnoty:
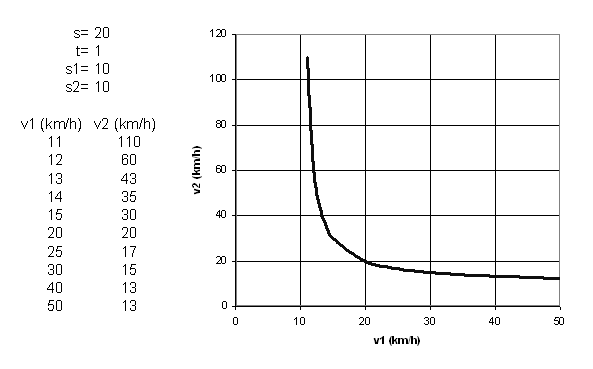
Jak je vidět, vztah není vůbec lineární a existují jistá omezení (asymptoty křivky v grafu). Jedním omezením je minimální rychlost pro druhý úsek - je to logické, kdyby člověk projel první úsek nekonečně rychle, stejně by musel jet druhý úsek hodinu (v našem příkladu je to 10 km/h). Druhé omezení je maximální čas, který cyklista může strávit na prvním úseku - pokud ho pojede moc pomalu a dojede před na jeho konec za určitý limitní čas (v příkladu je to 1h), nedokáže už v druhém úseku průměr spravit - ani kdyby jel nekonečně rychle.
Tož tak je to. A teď už zase do práce.