Obvod zeměkoule

23 duben, 2010

Vztah mezi poloměrem a obvodem kružnice dokáže pěkně potrápit to, čemu říkáme selský rozum. Následující příklad mě provází celý život a ani dnes, po tolika letech, jsem jeho řešení svým selským rozumem zatím nevstřebal. Takže:

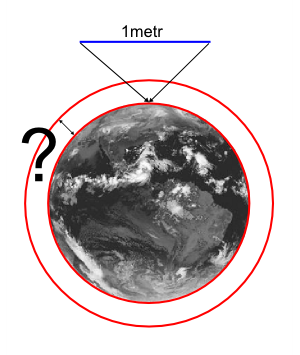
Zadání

Představte si zeměkouli a drát, který natáhnete po rovníku kolem dokola. Zjednodušme tvar země na ideální kouli - drát pak tvoří kružnici. Drát bude dlouhý přibližně 40 000 km a bude leže po celé své délce na zemi. Nyní drát v jednom místě přestřihneme a do místa střihu vložíme 1 metr nového drátu. Celková délka drátu se tak zvětší o jeden metr a drát se po celém obvodu zeměkoule nepatrně zvedne. Otázka zní. Zvedne se po celém obvodu od země tak vysoko, aby vzniklým prostorem kdekoliv prolezla myš?

Bude takový zdvih zanedbatelný, bude několik centimetrů nebo metrů?

Řešení

Odvození vztahu pro výpočet zdvihu je úplně jednoduché a výsledný vzoreček udivující. Co vlastně chceme spočítat: známe poloměr Země (r), obvod Země (2*pi*r) a délku vloženého úseku drátu. Zajímá nás změna poloměru kružnice tvořené drátem při změně délky obvodu. Odvození obecného vztahu je elegantní a důležité pro další úvahy. Takže:

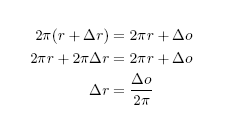
Na levé straně rovnice je vzorec pro výpočet obvodu prodloužené kružnice vyjádřený pomocí poloměru Země ( r) a změny poloměru, kterou si prodloužení vyžádá ( delta r). Na pravé straně je vzorec pro výpočet obvodu Země v součtu s prodloužením ( delta o - u nás 1 metr). Po pár úpravách dostaneme jednoduchý vztah mezi změnou obvodu ( delta o) a změnou poloměru ( delta r). Dosazením 1m za delta o dostaneme výsledek: 1 / 2 * pi, což je přibližně 15 cm.

To není vše. Obecný vzoreček, který jsme odvodili má zajímavou vlastnost. Úplně z něj vypadly členy obsahující skutečné rozměry Země. Znamená to, že vztah platí nejen pro Zemi, ale i pro libovolně velkou kružnici. Prakticky to znamená, že ať vezmete kružnici s poloměrem 1cm nebo 1 světelný rok, pak prodloužení jejího obvodu o jeden jediný metr způsobí rovnoměrný zdvih pomyslného drátu o 15cm. Vztah platí i pro bod - tedy nekonečně malou kružnici s nulovým poloměrem i obvodem. Když její nulový obvod zvětšíme o metr, poloměr bude našich patnáct centimetrů.

Komentáře

arny 2012/12/29
jj, tohle je mazec!
IIBB 2013/10/01
kamaráde mimochodem není divu, že ti to selský rozum nebere, protože tvoje matematická dedukce... je s prominutím "špatně" - zkus to jinak:)
- Michal N. 2013/10/01
  Dokud nenapíšeš co je špatně, tak nemám co zkoušet.
Jiří Valášek 2013/11/15
Ano, je to tak, ale take se s tim smiruji cely zivot. Tesi me, ze nejsem sam. Jirka
Jan Navrátil 2014/08/13
Nedávno mi tuto úlohu taky někdo dal a taky jsem si říkal, že to není možné, aby byl ten rozdíl znatelný a myš tam prolezla, i když matematicky to sedělo. Za dva dny mě to napadlo. "Zaokrouhlil" jsem si obvod Zeměkoule na čtverec :o) a už jsem si to představit dokázal. Přidáním 1 metru k obvodu libovolného čtverce je rozdíl mezi hranami 12.5 cm (na rozích víc). Na základě čehož jsem si dovolil vyslovit postulát: Člověku se lépe přemýšlí hranatě než kulatě. :D
- Michal N. 2014/08/14
  Nechu být kverulant, ale mám pocit, že čtverec místo kružnice pochopení nijak neulehčí. Když prodloužíš obvod libovolného čtverce o 1m, změní se délka každé strany o jednu čtvrtinu metru - tedy o 25cm. Když to použiješ na zeměkouli - tak představa, že přidáním jednoho metru se čtverec po celém svém obvodu zvedne o 12,5cm je, alespoň pro můj selský rozum, úplně stejně nepřijatelná jako u té kružnice.
Jan Navrátil 2014/08/14
No pro lepší představu se asi dá říct, že u každé ze 4 stran čtverce se prodlouží oba 2 její konce, aby se od původního rovnoměrně vzdálil. Takže při tomto způsobu připojení se metr rozdělí na 8 částí. Oddálí se tedy o 1 m / 8 = 12,5 cm. A tato vzdálenost není závislá na původní velikosti čtverce. Dobře by to šlo vidět na obrázku.
carbocit 2014/10/21
Nejsem matematik a tak jsem si dovolil použít právě ten selský rozum neboť již ze školy si pamatuju,že se v rovnicích dělají chyby. Obvod Země je 40000000 metrů. Když ho vydělím 3,14 dostanu průměr 12738853,503 metrů. Zvětšený obvod je 40000001 metrů vydělím opět 3,14 což je 12738853,82. Ta čísla za destinou čárkou jsou 50 a 82 centimetrů,což je rozdíl 32 centimetrů a ne 15 !!! Koule s obvodem 10 metrů má průměr 318 cm. Koule 11 metrů má průměr 350 cm. Kde je těch zázračných 15 centimetrů ?
- Michal N. 2014/10/21
  Já taky nejsem matematik, ale: 1. Průměr není poloměr, na to pozor. Vy jste počítal s průměrem, takže i těch vašich 32 centimetrů je přírustek průměru, ne poloměru. Přírustek poloměru (tedy to o kolik se zvedne drát rovnoměrně po celém obvodu zeměkoule) je polovina z těch 32, tedy 16. O centimetry už se asi hádat nemusíme - zkuste si to spočítat s přesnějším vyjádřením čísla pi. 2. Proč jste nedopočítal přiklad s tou malou koulí? Udělám to tedy za vás: 10 / 3.14 = 3.185, 11 / 3,14 = 3.503, když čísla od sebe odečtu, dostávám 0,318, což je opět přírustek průměru v metrech. V centimetrech je to 31,8. No a protože je to opět průměr, tak přírustek poloměru je oněch zázračných 31,8 / 2 = 15.9 centimetrů. Žádná velká matematika to není, stačí používat právě ten selský rozum.
Honza Hejduk 2015/05/15
No..zvedlo se to o 1.59 mm ..né o 15.9 cm :D
- Michal N. 2015/05/15
  Milý Honzo, jsi jeden z moha, kdo to zkouší. Napsat nějaký nesmysl dokáže každý. Jestli máš chuť mé závěry zpochybňovat, tak pošli svůj výpočet nebo ukaž místo, kde je chyba. Jinak je tvůj příspěvek zcela bezvýznamný.
Radim 2016/03/01
Jo, je to tak. Tuto úlohu si pamatuji z matematické olympiády pro středoškoláky někdy v r. 1969.
Jirka 2017/01/10
Selský rozum mě říká, že na každej metr obvodu připadá 32 cm průměru. Problém vidím v tom, představit si 40 000 km :-)
Josef 2017/10/11
Toto je velmi stará úloha, četl jsem ji kdysi v nějakém starém VTM (hodně starém, padesátá či šedesátá léta). Akorát tam tenkrát bylo přidáváno 10 metrů a ne jeden (přitání těch 10m cílilo právě na to, že v uváděném obvodu se selským rozumem i toto zdálo naprosto zanedbatelné). Zvýšení drátu v tom starém příkladu pak bylo o 159 cm (takže jest otázkou, jestli si třeba Honza Hejduk nepamatuje stejný příklad ;-) a jen si nepřečetl pečlivě zadání tohoto, kde se přidává pouze metr). Jinak já sám preferuji ten příklad s přidáním 10 metrů a pak "ohromujícím sdělením" že by to podlezla nejen myš, ale klidně i člověk (by se musel trochu sehnout, pokud by měřil více jak těch 159cm... ;-))
- Michal N. 2017/10/11
  Já to mám taky ze staré knihy, kterou mi dal kdysi před 30 lety můj děda. Podobných tam bylo spousta (např. výpočet PI házením jehly na papír s čárama). Tahle se mi zdála nejzajímavější.
Josef 2017/10/11
Uff, teď koukám, že i já si blbě přečetl co Honza nasal, on psal 1.59mm a ne 1.59m... Už taky blbě vidím...
Josef 2021/02/08
Na 40.000 km přidat jeden metr nezvedne tzv.drát okolo zeměkoule o 15cm ...to je selský rozum! Ale na druhou stranu matematika mluví jasně ...drát bude o cca 15 cm nadzvedlý! Jen ten selský rozum se s tím hůře smíří :-)
Jarda 2021/05/25
To se dá odvodit selským rozumem bez nějakého počítání s pí. Kruh při takových rozměrech je lokálně prakticky přímka. Vezmu metr rovného drátu a budu jej přidávat po čtvrtinách, vždy dva kusy a dva kusy najednou. Nejdřív kruh přepůlím a na každou stranu vložím 25 cm (1/4 z metru). Abych jej mohl vložit a udělat tuto mezeru, musím ty dva půlkruhy na každé straně nadzvednout o 12,5 cm. Tzn. že se mě nahoře a dole nadzvedne od země o 12,5cm. Totéž udělám u dalších dvou řezů a mám to.

Věda nevěda